geogebra图形计算器软件 5.2.884.1手机最新版

geogebra是一款图形制作以及计算的动态数学软件，在校园的教育课堂中，数学往往对大多数人来说都是一门比较枯燥而且特别消耗时间的学科，但是这门学科无论是在校园还是在以后的生活中又无比的重要。这款软件确实很多人都用了都说不错，值得推荐哈。

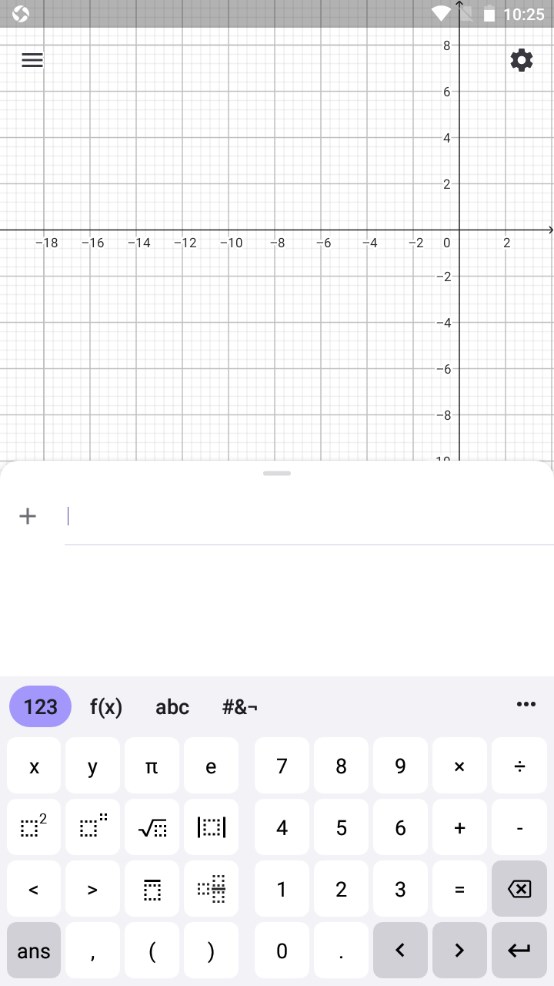
图形计算器怎么用

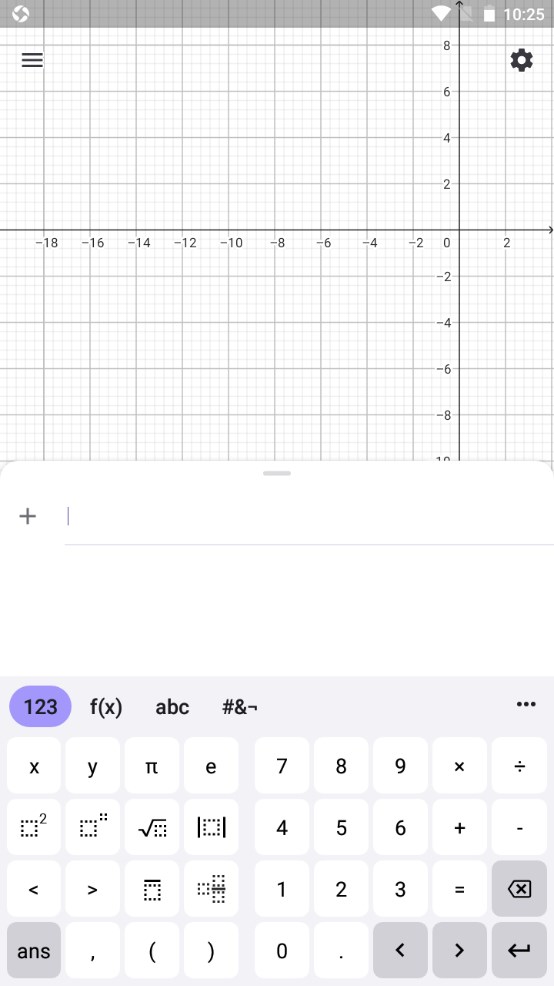
1.打开图形计算器，点击空白处切换到代数区。

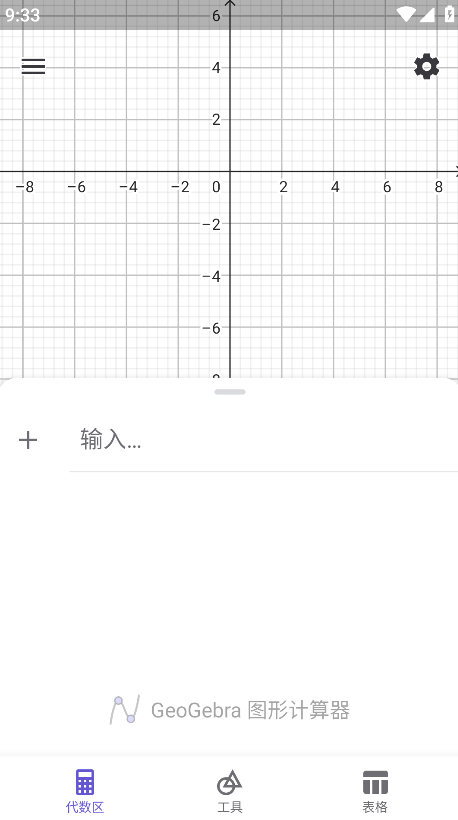
2.点击+。

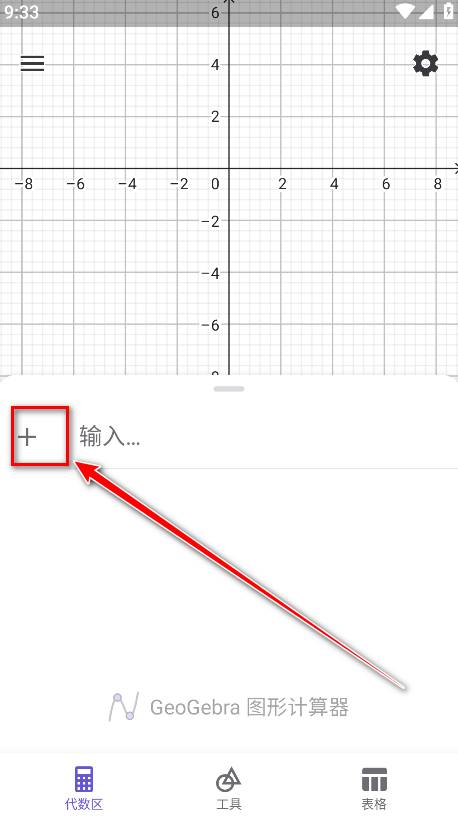
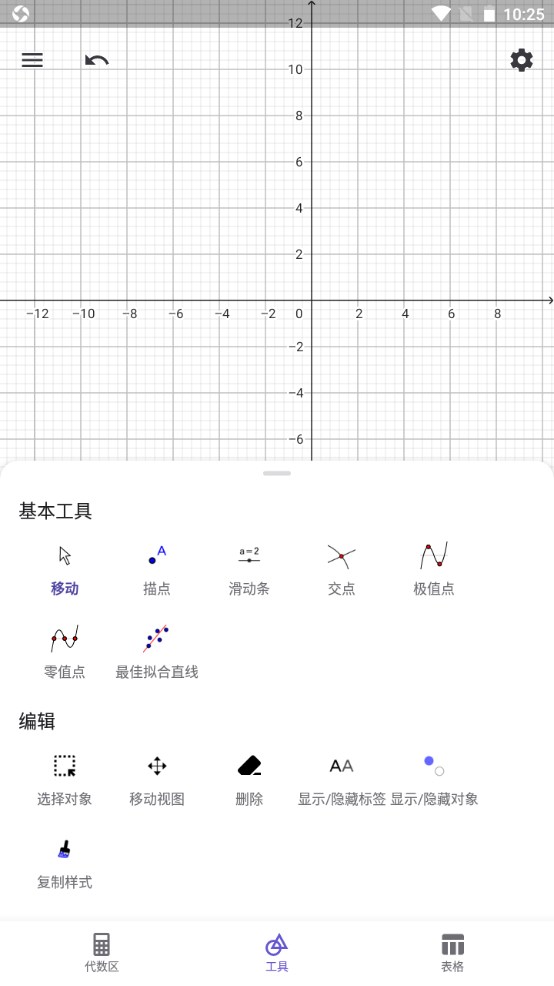
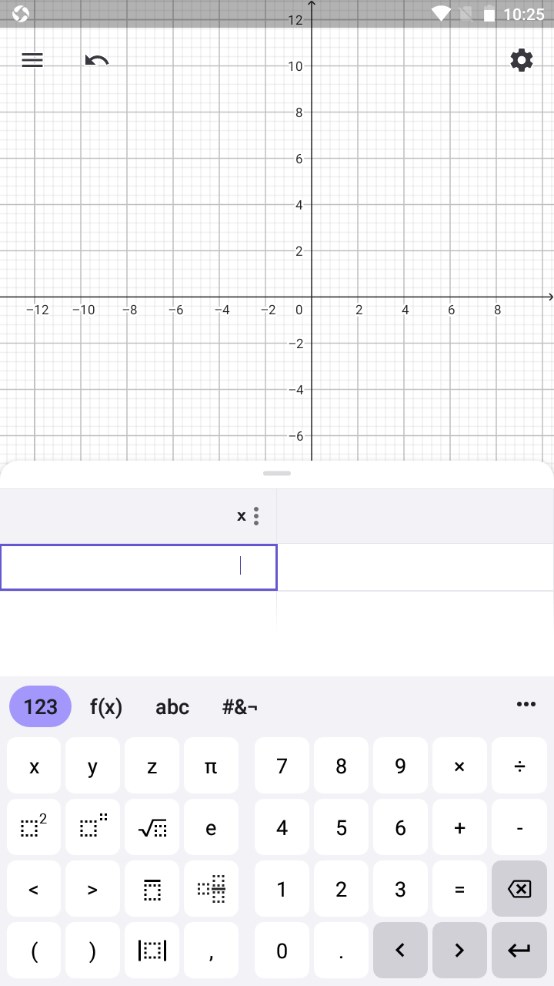
3.点击代数式。

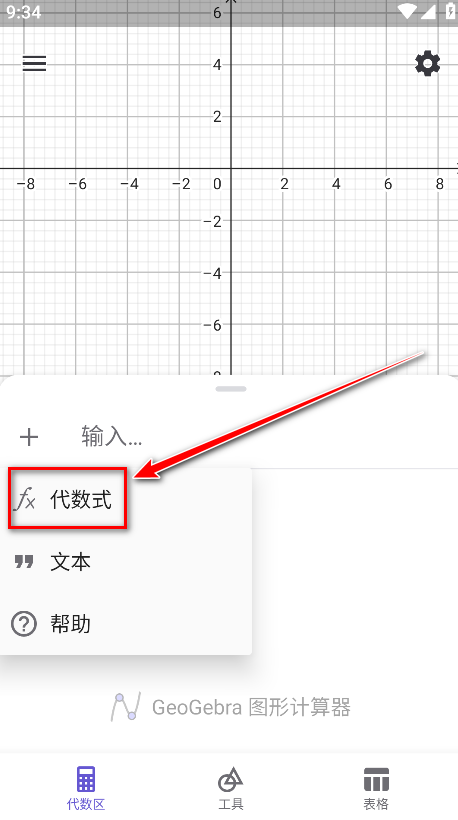
4.接着直接在加号图标右侧进行输入，这里我们输入f(x)=x2函数，输入之后可以看到图中出现了相应的图像。

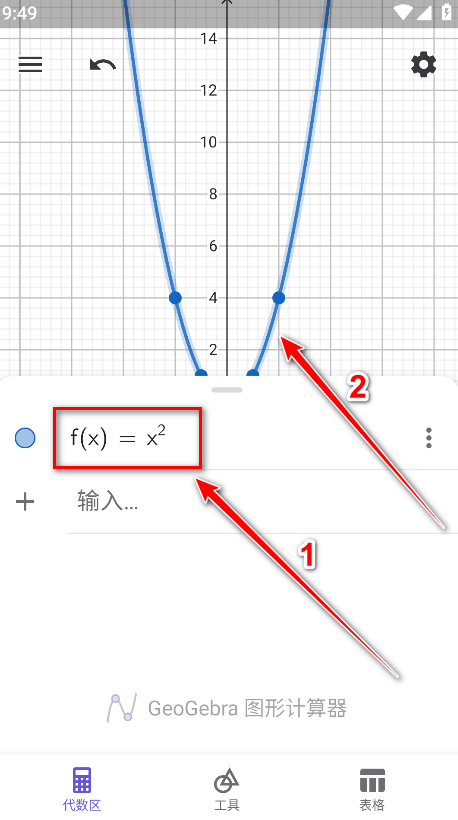
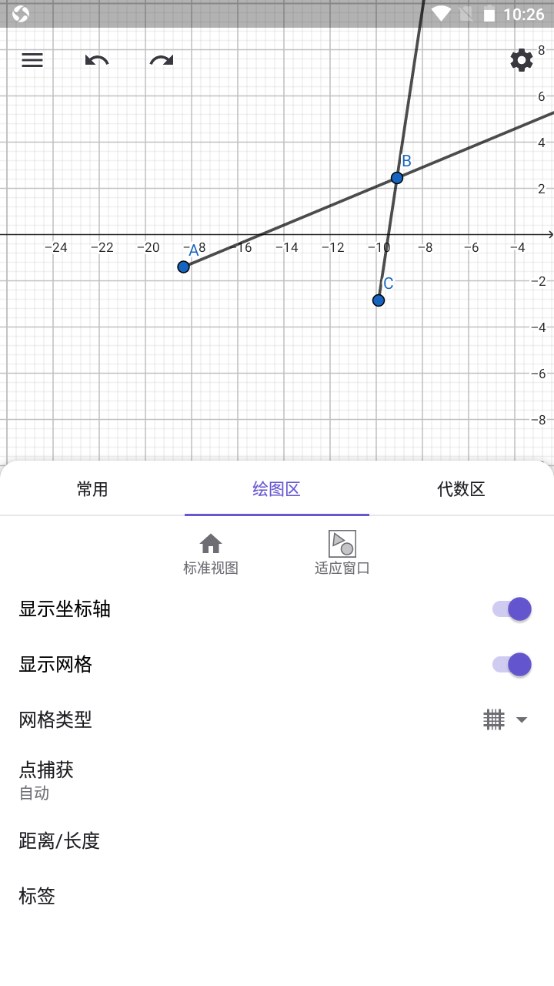
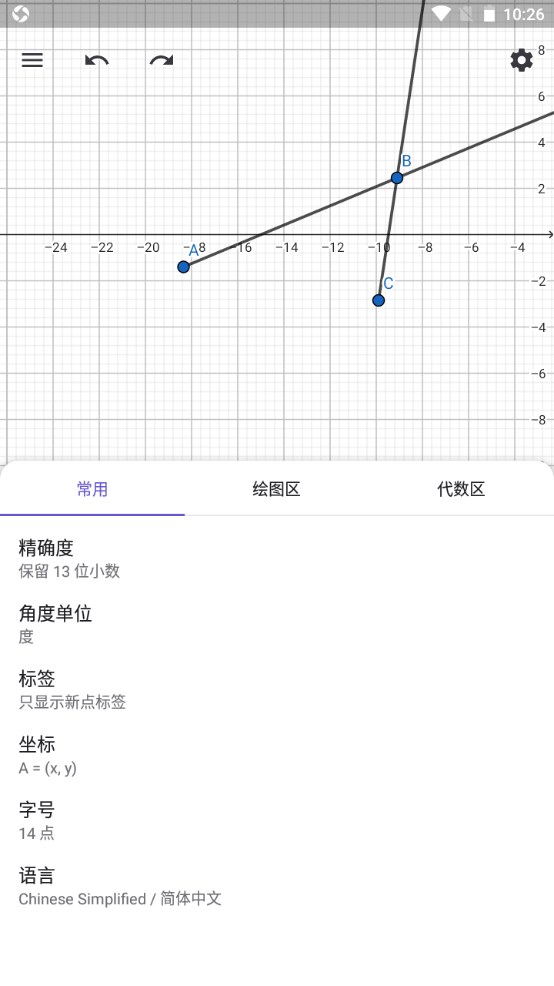
5.如果绘图区中没有显示网格和坐标轴，可以点击右上角的设置。

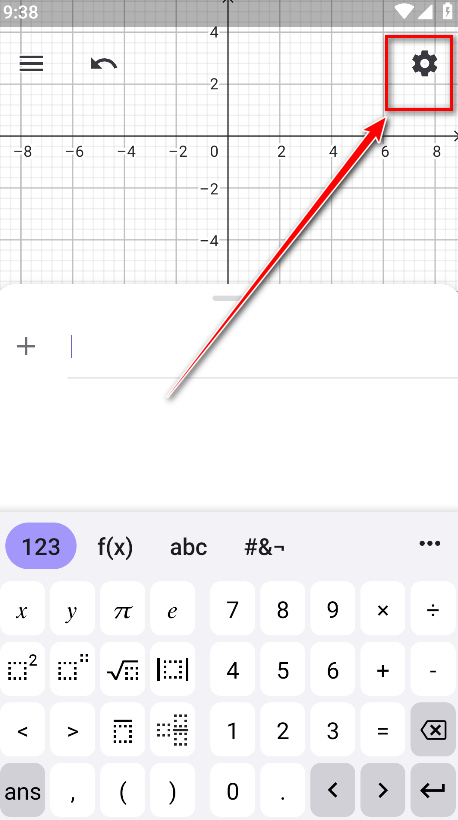
6.选择并开启显示坐标轴、显示网格。

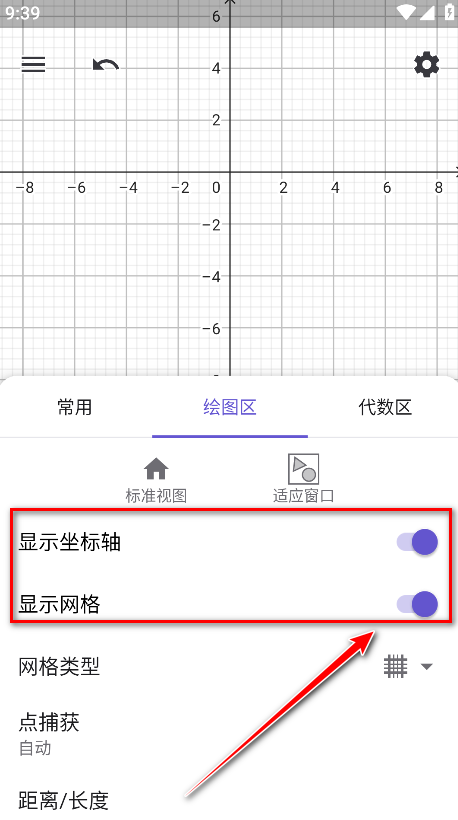
7.点击该函数右边的三个小点，然后点击数值表。

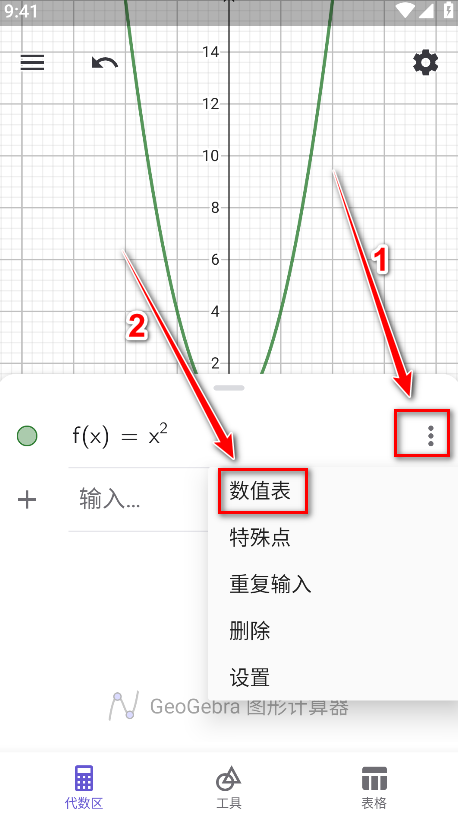
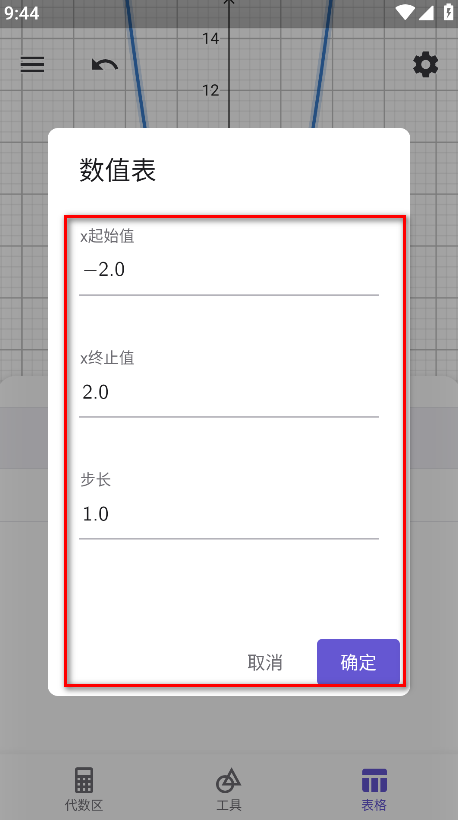
8.请设置自己想要的数值，然后点击确定。

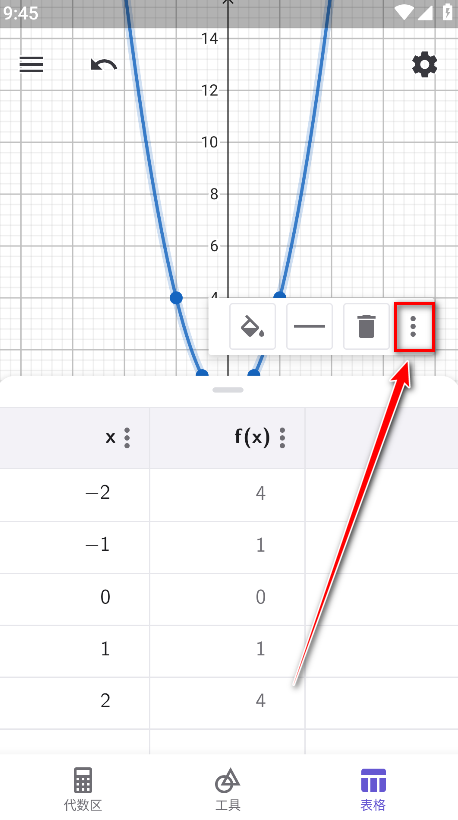
9.当你选中并点击函数之后，点击旁边的三个小点。

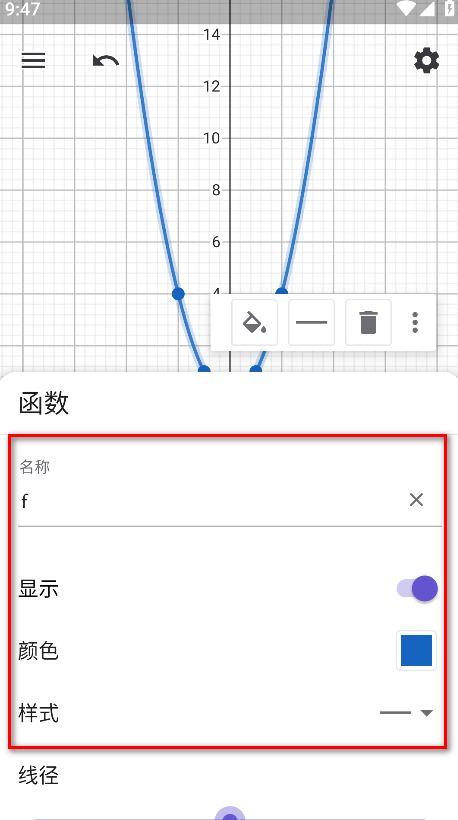
10.可以在弹出的选项中对函数名称、颜色、样式等进行更改。

geogebra怎么输入参数方程

1.打开Geogebra软件并创建一个新的工作表。

2.在工作表上选择适当的坐标系。对于平面上的参数方程，可以选择坐标轴为x轴和y轴的直角坐标系。对于三维空间中的参数方程，可以选择具有x轴、y轴和z轴的直角坐标系。

3.在输入框中输入参数方程。参数方程的形式可以是x=f（t）和y=g（t），或者在三维空间中为x=f（t），y=g（t）和z=h（t）。

4.使用滑动条或手动输入参数的值来观察图形的变化。Geogebra将自动计算并显示与参数相关的坐标点。

5.可以通过设置参数的起始值和终止值来控制图形的范围。这样可以观察到参数取不同值时图形的变化。

6.可以使用其他Geogebra命令和工具对参数方程进行进一步的分析和操作。例如，可以使用导函数命令计算参数方程的导数，从而获得速度和加速度的信息。

参数方程在几何学中可以用来描述各种曲线，如直线、抛物线、椭圆、双曲线和螺旋线等。在物理学中，参数方程可以描述运动的路径，如自由落体、抛体运动和行星运动等。在工程学和计算机图形学中，参数方程常用于描述曲线和曲面的形状。

下面我们将以三维空间中的参数方程为例来进行详细说明。

假设我们有一个运动的粒子，其位置在三维空间中由参数方程x=f（t），y=g（t）和z=h（t）描述。其中，堤是时间参数，而x、y和z是与时间相关的坐标。

例如，我们可以使用以下参数方程来描述一个简单的螺旋线：

x=cos（t）

y= sin（t）

z=t

在Geogebra中，我们需要按照上述步骤来输入这个参数方程并观察图形的变化。

首先，我们选择一个三维坐标系，并输入参数方程。然后，我们可以使用滑动条来改变参数t的值，并观察图形的变化。可以注意到，由于参数方程中的三个坐标都与参数t相关，因此图形将在三维空间中沿螺旋线路径运动。

此外，我们还可以对参数方程进行其他操作。例如，我们可以使用导函数命令来计算参数方程的导数，从而获得速度和加速度的信息。可以使用曲面命令来创建参数方程所描述的曲面。还可以使用其他Geogebra工具对图形进行更详细的分析和操作。

通过使用Geogebra中的参数方程功能，我们可以更直观地理解各种数学和物理现象，并将其应用于实际问题的求解。它为学生和教师提供了一个直观、动态且交互性强的学习工具，使他们能够更好地理解和应用参数方程的概念。